Volatility is a measure of risk. It describes how far a commodity will most probably move within a given period of time. The most common measure for volatility is historical volatility. But I do not like the complicated formula for standard deviation.
There has to be a better way to explain and calculate volatility….
Implied Volatility
The options market has got a perfect measure for volatility. Done without formulas, just by demand and supply. And as I believe in efficient markets, the option markets fair price for volatility will be my starting point.
To get the price for volatility at the option market you just have to place a bet. Assume you want to know the (expected) volatility for the next 30 days, then you would just add the price for an at the money put and call with 30 days to expiry. Option traders call this bet a straddle, and you would win if the market moves more than the price you have payed for the (european style) put and call.
The fair price for a volatility bet
Implied volatility and this Straddle bet is the starting point to calculate my own volatility measure.
The fair price for this bet is, when neither the buyer nor the seller of the bet has got an advantage. In the long run it should be a zero sum game game for both of them. Calculating the fair bet price for a straddle is the idea behind my volatility measure.
Think about a simple coin flip game. If you bet on head you can either win 1€ if head is up or nothing if tail comes on top. What would be the fair price for such a bet?
As head and tail got the same probability, the expected return of a bet on head’s up would be 0.5€. If I would sell you a bet on the next coin flip, I would charge you this 0.5€ to make it a fair bet. So you would either lose the 0.5€ if tail’s up, or win 1€ -0.5€ if head’s up. In the long run this would be a zero sum game for both of us. Do the same thing for the tail is up bet. It also got a value of 0.5€.
Historical Volatility vs. Kahler’s Volatility:
Historical volatility uses standard deviation of daily log returns to describe the volatility of the market. The standard deviation of this +1 -1 coin flip experiment would be 1€. The same would be true if you would buy a head’s up and a tail’s up bet; it would also cost you 1€. So for this simple example the fair bet based volatility is the same as the historical volatility.
But the market is not a coin flip. There will be some differences between historical volatility and KVOL fair bet based volatility.
KVOL vs. historical volatility:
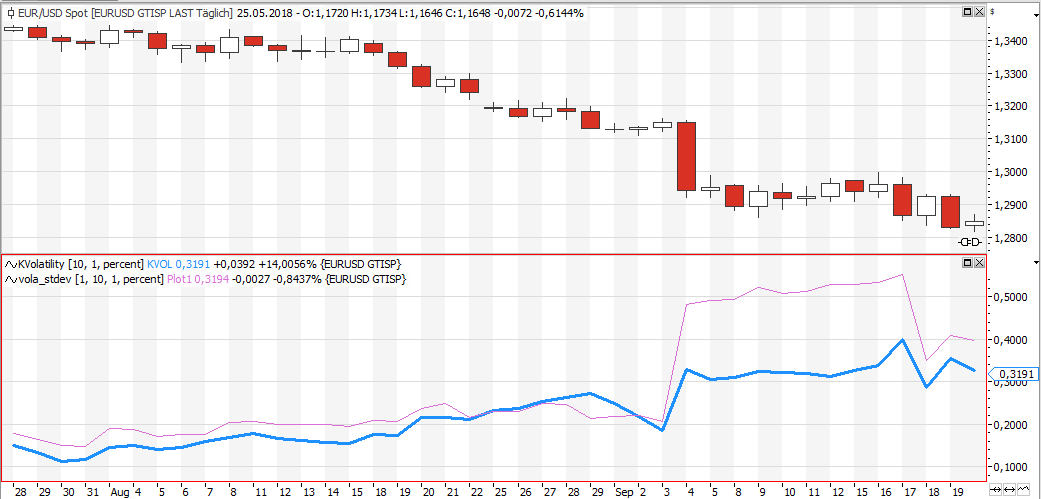
The chart shows you a comparison between KVOL (blue) and historical volatility (standard deviation). On the chart shown above both calculate the volatility for 10 day returns, using the previous 30 bars as data sample.
As you can see historical volatility and KVOL are highly correlated.
But there are some major differences:
As an example in the end of 2017/beginning of 2018 KVOL starts to rise as the market is exploding to the upside. This is due to the virtual call used to calculate KVOL gains value. At the same time historical volatility stays low, as the market has got one direction and no setbacks.
Another advantage of KVOL is it`s response to singular events. As you can see on Sept. 3rd on the chart above the singular big red candle leads to a spike in historical volatility. It also raises KVOL, but not as much. As both indicators are calculated over the same period of bars they both got the same speed of change, but when you have a look at the scale you will see the advantage of KVOL: Historical volatility jumps from 0.2 to over 0.5 – it more than doubles just because of a single event. KVOL also raises,but only from 0.2 to 0.3.
For me this mild response to to singular events is the main advantage. Imagine a portfolio based on value at risk – would it really be useful to half the exposure just because historical volatility jumps after a single red candle?
KVOL – Tradesignal Equilla Code:
The code to calculate KVOL is simple and straightforward.
The inputs:
multi: just a multiplier, like you can display 1 or 2 standard deviations..
datapoints: The number of bars used to calculate KVOL
returnperiod: calculate the volatility for 1,2,3… bars
showresult: show the result as a percentage of the underlying or as an absolute number
show: show either kvol or the rank of kvol within the last 100 bars. This gives an idea if volatility is high or low
Meta: subchart(true);
Inputs: multi(1.0), Datapoints(30), returnperiod(5), showresult(percent, absolute), show(result,rank);
Variables:Kvol, i, rp,rc, rpsum, rcsum, call, put, hh,ll;
rpsum=0;
rcsum=0;
for i =0 to datapoints-1 begin // loop over last bars
rc=maxlist((close[i]-close[i+returnperiod])/close[i+returnperiod],0); // % return of call
rp=maxlist((close[i+returnperiod]-close[i])/close[i+returnperiod],0); // % return of put
rcsum=rcsum+rc; // sum of all %returns over time
rpsum=rpsum+rp;
end;
call=rcsum/datapoints;
put=rpsum/datapoints;
Kvol=call+put;
if show=result then drawline(multi*iff(showresult=percent,100*Kvol,Kvol*close),"KVOL");
hh=highest(kvol,100);
ll=lowest(kvol,100);
if show=rank and (hh-ll)>0 then drawline(100-100*(hh-kvol)/(hh-ll),"rank");
keep researching…