the blog is closed and the domain quanttrader.com is for sale
Trading Strategies
The Edge of an Entry Signal
When developing a new trading strategy you are usually confronted with multiple tasks: Design the entry, design the exit and design position sizing and overall risk control. This article is about how you can test the edge of your entry signal before thinking about your exit strategy. The results of these tests will guide you to the perfect exit for the tested entry signal (entry-exit combination) Continue reading
The Probability of Normality
As an option seller you want the market to stay within the range prognosticated by implied volatility. But what is the historic probability that markets behave as expected? And what other analysis could be done to enhance your chances and find the periods when it is wise to sell an at the money straddle? This article will try to give some answers to this question.
The normal distribution cone
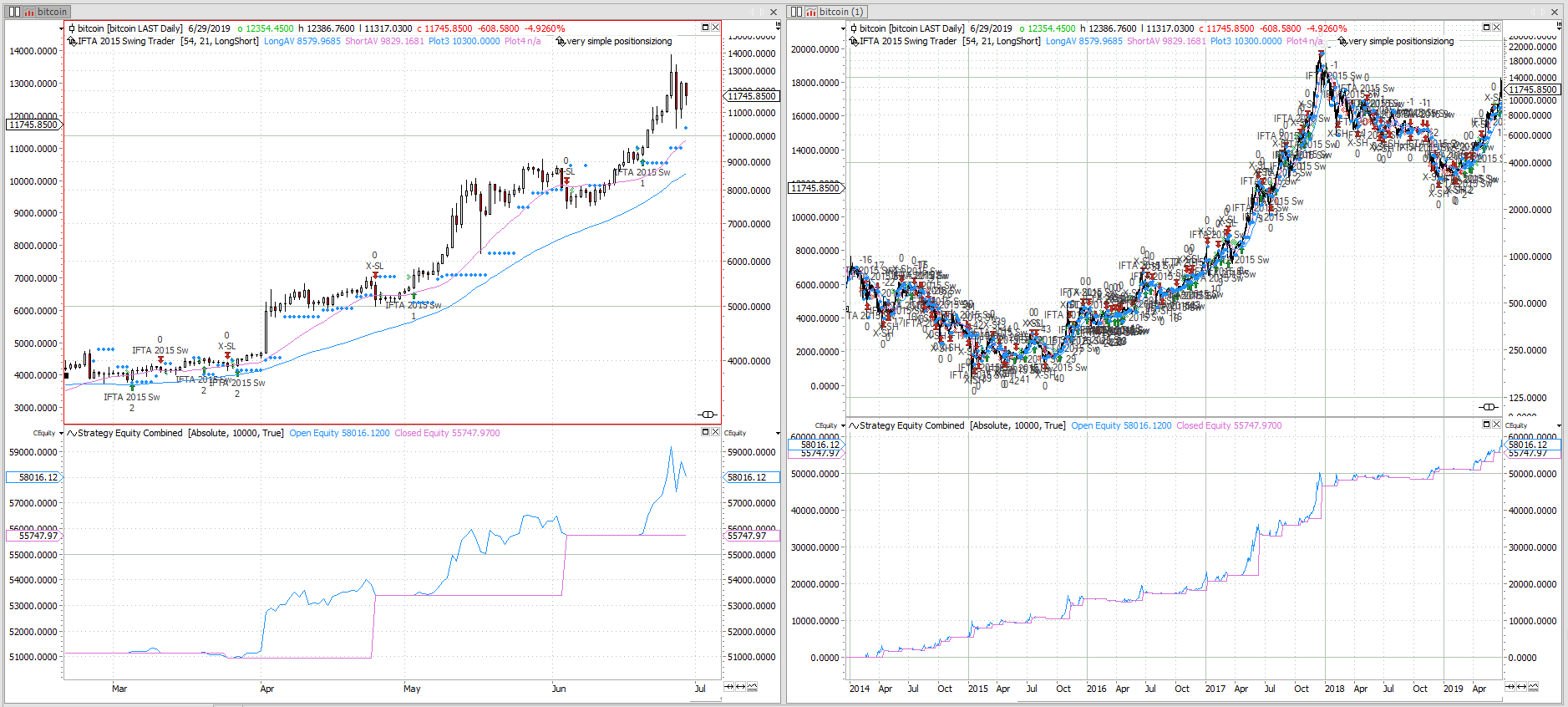
Bitcoin Swing Trading
I published a bitcoin swing trading strategy in 2015 over here (German only). Time to review the methodology of swing trading and have a look on the performance. Can a rational strategy get an edge in an irrational market? Have a look and be surprised! Continue reading
The Edge of Technical Indicators
Classical technical indicators like RSI and Stochastic are commonly used to build algorithmic trading strategies. But do these indicators really give you an edge in your market? Are they able to define the times when you want to be invested? This article will show you a way to quantify and compare the edge of technical indicators. Knowing the edge of the indicator makes it an easy task to select the right indicator for your market. Continue reading
Daily Extremes – Significance of time
Analysing at which time daily market extremes are established shows the significance of the first and last hours of market action. See how different markets show different behaviour and see what can be learned from this analysis.
Probability of Extremes
A day of trading usually starts with a lot of fantasies for the future, then we try to survive the day and end it with a lot of hope for tomorrow. This psychological pattern can also be shown when analysing intraday market data. A high level of fantasies usually leads to a strong market movement, and thus market extremes can often be seen near the beginning or the end of the trading session. Continue reading
S&P500 – when to be invested
The stock market shows some astonishingly stable date based patterns. Using a performance heat map of the S&P500 index, these patterns are easily found.
Date based performance
The chart below shows the profit factor of a long only strategy investing in the S&P500. Green is good, red is bad. The strategy is strictly date based. It always buys and sells on specific days of the month. Continue reading
Noisy Data strategy testing
Algorithmic trading adds noise to the markets we have known. So why not add some noise to your historic market data? This way you can check if your algorithmic trading strategies are fit for the future. Learn how to generate noisy data and how to test your strategies for stability in a noisy market.
Synthetic market data?
Monte Carlo Simulation of strategy returns
Monte Carlo Simulation uses the historic returns of your trading strategy to generate scenarios for future strategy returns. It provides a visual approach to volatility and can overcome limitations of other statistical methods.
Monte Carlo Simulation
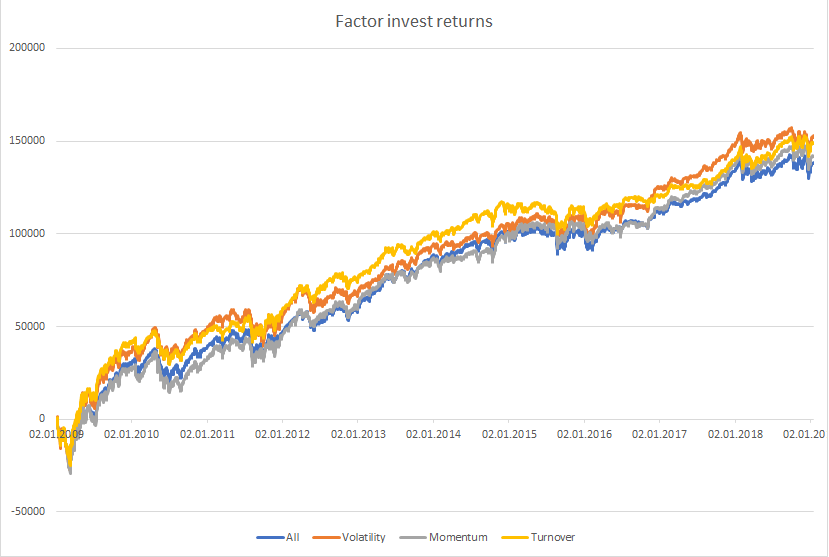
Factor investing in portfolio management
Factor investing has been around in portfolio management for some years. Based on algorithmic rules it became the big thing in trading and the ETF industry. But is there still some money to be made? Is small beta still smart or just beta? This article will give you a Tradesignal framework to test the factor investing ideas by your own. Continue reading
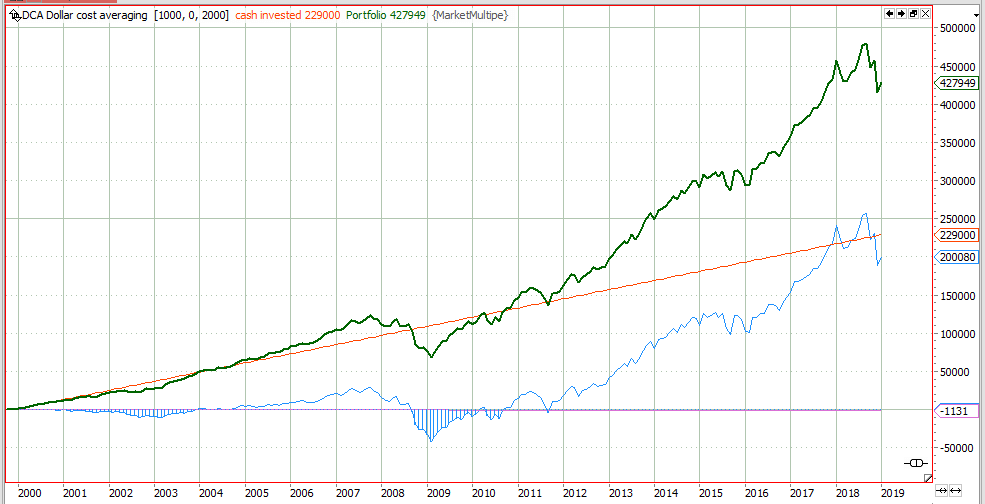
Dollar Cost Averaging Investment Strategy – success based on luck?
This article is about the dollar cost averaging investment strategy and the influence of luck in it. Continue reading
Bullish? Buy stock or sell put option?
So you are bullish on a specific stock, but you also have realised that timing is major problem? So what would be the best strategy to implement your bullish opinion but avoid the problems of any timing strategy?
Selling a put option might be the answer. Continue reading
An Algorithmic Stock Picking Portfolio
In this article I will discuss a simple algorithmic stock picking approach based on momentum and volatility. The goal will be to generate excess returns versus a capital weighted stock basket. Continue reading
Bollingerband: The search for volatility
Usually it makes no sense to fight against normal distribution. But there are setups which have got a high probability of unexpected behaviour. Volatility can be the key to future market movements. Continue reading
Tradesignal Implied Volatility and IV Percentile Scanner
Implied volatility data is key in options trading. This article shows how to access free volatility data in the Tradesignal software suite. Continue reading
IV Percentile – when to sell volatility
Volatility trading: when to buy and when to sell volatility Continue reading
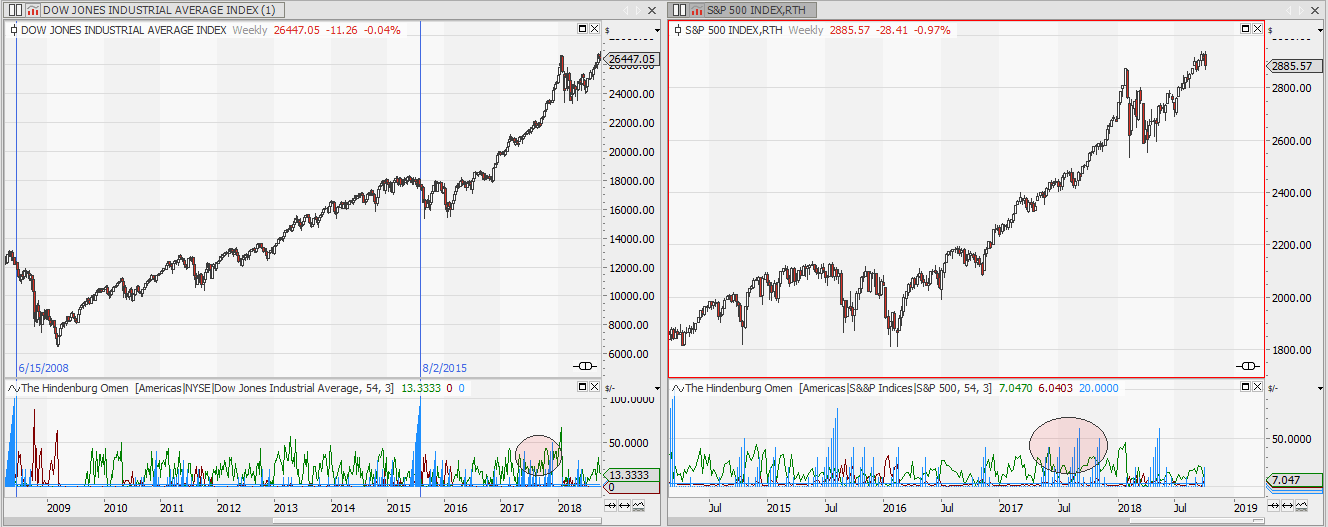
The Hindenburg Omen – Stock Market Crash Ahead?
The Hindenburg Omen is an indicator which is believed to forecast market crashes. Unfortunately it does not work, but the idea behind this indicator is worth to be discussed. Continue reading
Implied vs. Realized Volatility for NASDAQ100 stocks
(1) You shall only trade when the chances are on your side Continue reading
Scanning for Support and Resistance Probabilities
I have been in search for a signal I could use for a short vertical spread or naked short option strategy. So my main concern has been to find a level, which will most probably not be penetrated over the next few bars.
This is what I came up with. Continue reading
Backtesting Market Volatility
If you want to trade volatility, you can place a bet on the option market. Just buy an at the money put and call, and at expiry day you will either win or lose, depending on the actual market move since you bought the straddle and the price you paid for the straddle. To put it simple, if the market moves more than you paid for the two options you will win, otherwise you will lose. This article is about a back test of volatility. Continue reading