I published a bitcoin swing trading strategy in 2015 over here (German only). Time to review the methodology of swing trading and have a look on the performance. Can a rational strategy get an edge in an irrational market? Have a look and be surprised! Continue reading
Strategy
The Edge of Technical Indicators
Classical technical indicators like RSI and Stochastic are commonly used to build algorithmic trading strategies. But do these indicators really give you an edge in your market? Are they able to define the times when you want to be invested? This article will show you a way to quantify and compare the edge of technical indicators. Knowing the edge of the indicator makes it an easy task to select the right indicator for your market. Continue reading
S&P500 – when to be invested
The stock market shows some astonishingly stable date based patterns. Using a performance heat map of the S&P500 index, these patterns are easily found.
Date based performance
The chart below shows the profit factor of a long only strategy investing in the S&P500. Green is good, red is bad. The strategy is strictly date based. It always buys and sells on specific days of the month. Continue reading
Noisy Data strategy testing
Algorithmic trading adds noise to the markets we have known. So why not add some noise to your historic market data? This way you can check if your algorithmic trading strategies are fit for the future. Learn how to generate noisy data and how to test your strategies for stability in a noisy market.
Synthetic market data?
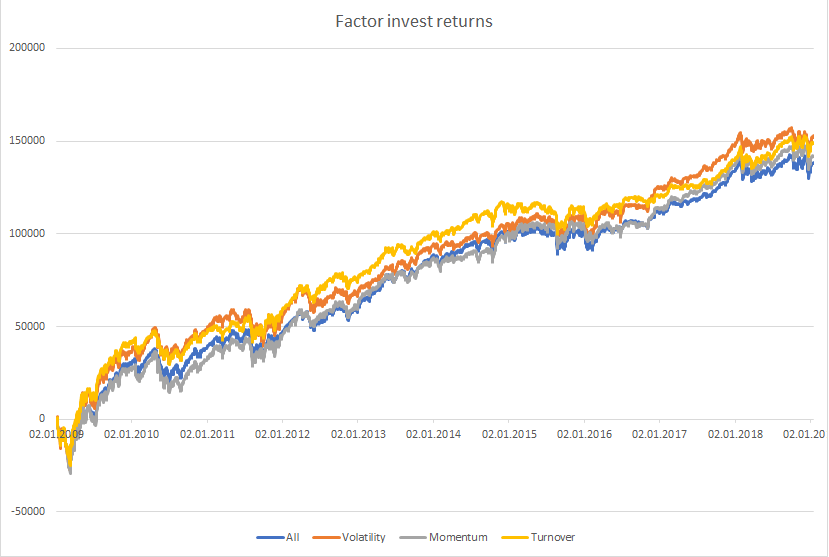
Factor investing in portfolio management
Factor investing has been around in portfolio management for some years. Based on algorithmic rules it became the big thing in trading and the ETF industry. But is there still some money to be made? Is small beta still smart or just beta? This article will give you a Tradesignal framework to test the factor investing ideas by your own. Continue reading
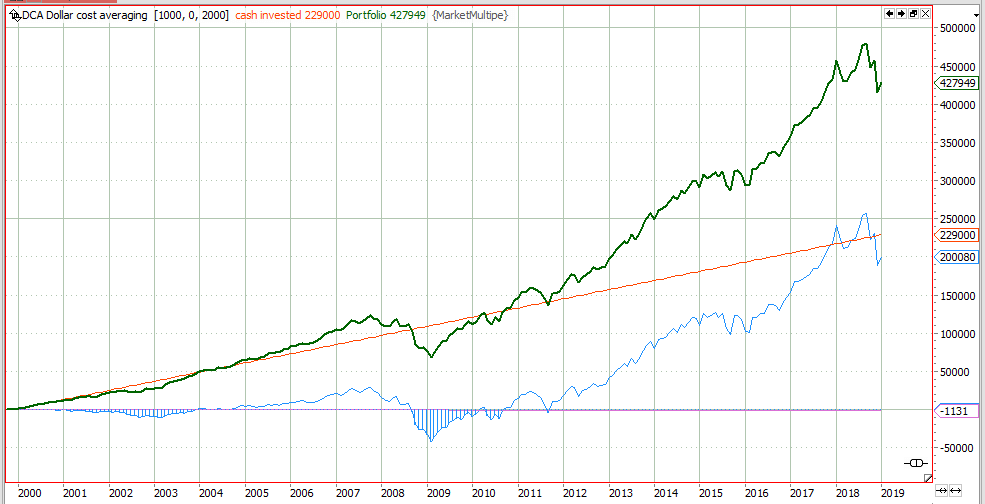
Dollar Cost Averaging Investment Strategy – success based on luck?
This article is about the dollar cost averaging investment strategy and the influence of luck in it. Continue reading
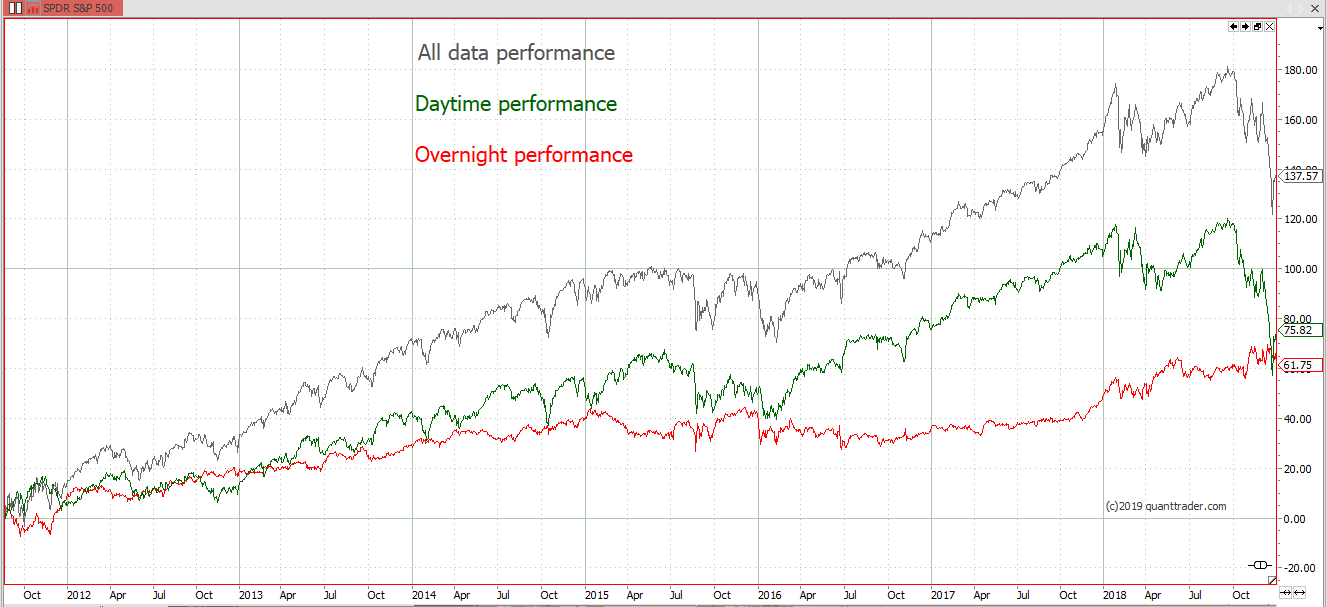
Overnight vs Daytime Performance & Volatility
Analysing the market performance of the day session vs. the overnight movement reveals some interesting facts.
Daytime vs. Overnight Performance
Technical vs. Quantitative Analysis
“The stock market is never obvious. It is designed to fool most of the people, most of the time” Jesse Livermore Continue reading
An Algorithmic Stock Picking Portfolio
In this article I will discuss a simple algorithmic stock picking approach based on momentum and volatility. The goal will be to generate excess returns versus a capital weighted stock basket. Continue reading
Bollingerband: The search for volatility
Usually it makes no sense to fight against normal distribution. But there are setups which have got a high probability of unexpected behaviour. Volatility can be the key to future market movements. Continue reading
Scanning for Support and Resistance Probabilities
I have been in search for a signal I could use for a short vertical spread or naked short option strategy. So my main concern has been to find a level, which will most probably not be penetrated over the next few bars.
This is what I came up with. Continue reading
A graphical approach to indicator testing
A graphical approach to indicator testing
The first step in algorithmic strategy design usually is to find some indicators which give you an edge and tell you something about tomorrow’s market behaviour. You could use a lot of statistics to describe this edge, but I like to take a graphical approach in indicator testing first, and only later on worry about the maths and statistics.
Scatter Charts
A scatter chart is a simple to read chart style to see the correlation between two input values. A regression line on the scatter chart gives you a visual idea if the two securities are positively or negatively correlated, the “cloud structure” of the scatter points tell you if this correlation is tight or loose.

This sample scatter shows the correlation between the DAX and DOW levels, and it can be easily seen that these two markets are tightly correlated in a positively way.
The horizontal scale is used for the second security (DAX), the vertical scale is used for the first security (DOW). This chart type is predefined in Tradesignal, just drag&drop it onto the securities on the chart and select the right amount of data to get the analysis you want to see. (eg. 2000-now). If you see a tight and positive correlation like on the chart above, It might be used to select the instrument you want to trade. If market A is easier to predict than market B, select A.
Scatter on Indicators
Although a scatter chart is usually used to show the correlation between two markets, it can also be used to show the correlation between two indicators.
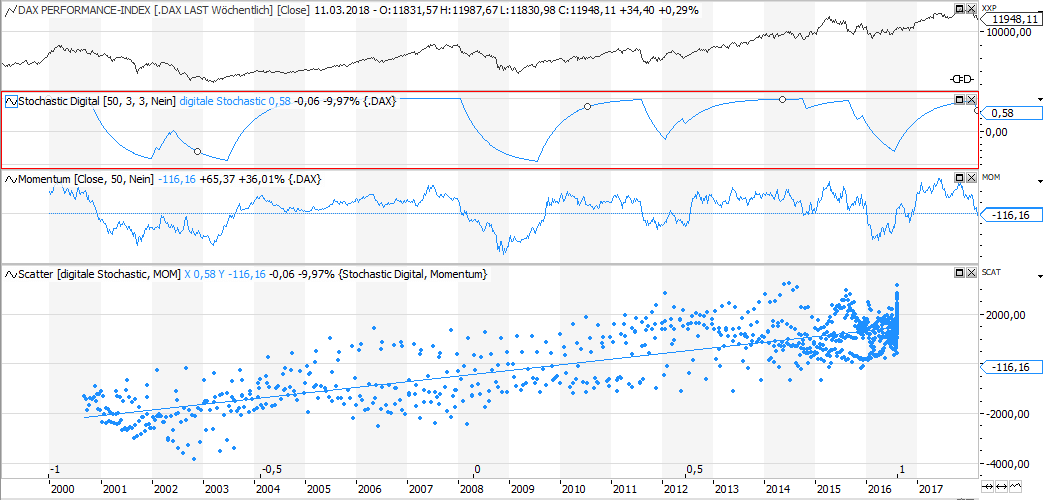
The chart above shows the correlation between digital stochastic and momentum. Have a look at the clustering of points in on the right side of the scatter, a high level in digital stochastic usually goes with a high momentum. This insight enables you to get rid of momentum, as digital stochastic is easier to read than the shaky momentum. Less indicators = less parameters = less curve fitting.
Scatter prognosis
Doing this analysis and getting rid of parameters is great if you want to minimise the dangers of curve fitting, but it does not tell you if your indicator is of any use at all, when it come to describing tomorrows move of the market. Surely it is valuable insight that a high level of stochastics corresponds to a high momentum, but does a high momentum today also mean that the market will move up tomorrow? And this question about tomorrow is the key question I ask myself when searching for some edge.
To get a glimpse on the prognosis quality of an indicator we will have to add some colour to our scatter chart. This colour tells me what the market has done after a specific indicator level has been reached. Green for an up move, red for a down move, black for not decided by now.

This chart shows the prognosis quality of the stochastic indicator. The left chart shows the 1 day prognosis of a 5 day stochastic, the right chart gives you the 5 day prognosis of a 21 day stochastic. Observe the clustering of the red and green dots. (black for not decided by now) As you can see on the left chart, the one day prognosis using a 5 day stochastic is not the thing to do. Regardless if stochastic is high or low, you get a nice mixture of red and green dots. This means the market, at a given stochastic level, sometimes moved up, sometimes moved down. Not this behaviour is not very useful for trading. Only in the extreme, near 0 and 100, this indicator seems to implicate a bearish next day movement.
The right chart, showing the longer term prognosis of a long term stochastic seems to be more useful. High levels of the indicator also show positive returns on the 5 days after, unfortunately you can not reverse the logic, as low indicator levels give a rater mixed prognosis. This visual analysis can give you an idea which areas of the indicator might be useful for further analysis.
A one dimensional analysis like on the chart above could also be done without this scatter chart. Going from one dimension to two dimensions is more useful, as it directly can be translated to do a kNN machine learning trading strategy. Have a look at the following chart. It shows the scatter of two indicators and the implication on the next days market move.
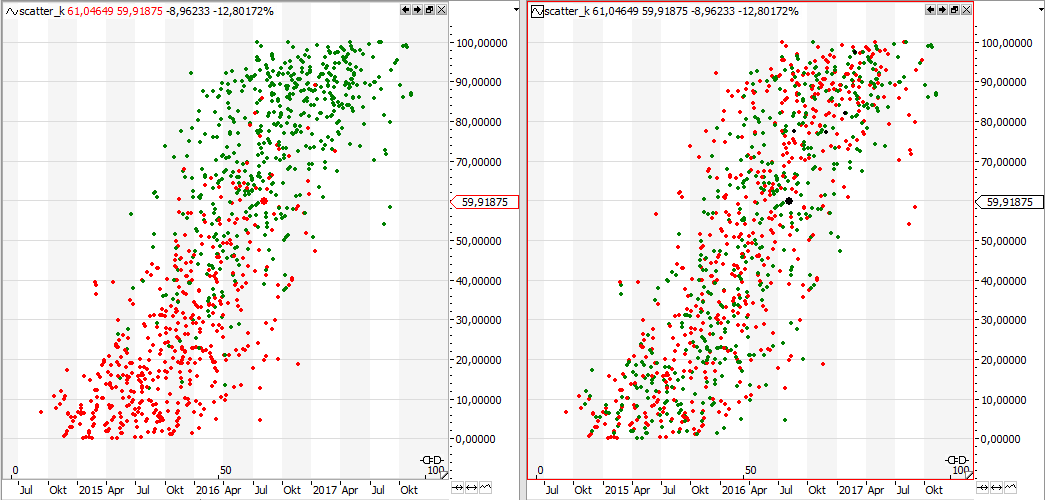
Lets start with he right chart. As you can see the red and green dots are evenly distributed, meaning there is no useful correlation between the used indicators and the movement of the market on the day after. If you would use a kNN algorithm with these two indicators, I would bet it would not return great results. Even if you would get a positive return, it might just be a lucky hit or curve fitting.
The opposite is true for the chart on the left. Here you can see some nice clustering of the red and green dots. Low indicator levels seem to predict a bearish move, high indicator levels result in a bullish move on the next day. A distribution like this is the perfect starting point for investing some time in a kNN machine learning trading strategy. The kNN algorithm would give you a strong prognosis with high or low indicator levels, and most probably only a weak or no prognosis when the indicators are around 50. The returns will be stable, no curve fitting problems should be expected.
Conclusion
Using a scatter chart can give you a nice visual indication if your indicator might be useful for a prognosis of the next days market move. This is valuable insight, as you can see the whole data universe with one glimpse, even before you do a thoroughly statistical analysis. Numbers can deceive you, pictures usually tell the complete story.
Tradesignal Equilla code:

Machine learning: kNN algorithm explained
I always thought that inspiration and experience are key factors in trading. But every time my chess computer beats me without any inspiration, just by brute force, I get my doubts. This article will be about a brute force approach in trading. The kNN algorithm.
Rule based trading
Rule based trading – algorithmic trading, is just a name for a set of if..then rules which will define the machines trading decisions. e.g. if the market crosses below the 200 day line, then short 100 contracts. If the market rises by 2% then exit the position. Easy stuff like this… (for the beginning)
This article will be a short introduction to machine learning. I will use a classic algorithm of machine learning to let my computer find a prediction for tomorrows market move. In the meantime I’ll have a glass of wine with some friends and let the machine do the job; At least that’s the idea, but can it be that simple in real life trading?
Unsupervised machine learning – kNN algorithm
The kNN algorithm is one of the most simple machine learning algorithms. Learning, in this case, is only a nice sounding label, in reality kNN is more of a classification algorithm.
This is how it woks:

The scatter chart above is a visualisation of a two dimensional kNN data set. For this article I used a classical indicators of technical analysis to do the prediction: a long-term and a short-term RSI indicator. The dots on the two dimensional scatter chart represent the historic RSI values at a given point of time.
Now have a look at the fat circled point. This point represents today’s value. It means, that today’s RSI1 has a value of 63, and RSI2 got a value of 70.
Additionally to the position on the chart the dots have got colours. A green dot means that the market moved up on the following day, a red dot shows a falling market on the day after.
We already know what has happened in history, so it is easy to colour the historic dots. But we do not know the colour of today’s dot, as it is not known where tomorrow’s market will end.
Based on the chart above, will it be a red or green dot? Will tomorrow be up or down? Should I go long or should I go short?
kNN – k nearest neighbours
To do a prediction of tomorrow’s market move, the kNN algorithm uses the historic data shown on the scatter plot above and finds the k-nearest neighbours of today’s RSI values. As you can see, our current fat point is surrounded by red dots. This means, that every time the two RSI values have been in this area, the market fell on the day after. That’s why today’s data point is classified as red. Wish it would be that easy all the times…
Call it classification or prediction, the two dimensional kNN algorithm just has a look on what has happened in the past when the two indicators had a similar level. It then looks at the k nearest neighbours, sees their state and thus classifies today point.
kNN as Tradesignal Equilla Code
In this article I would like to show you an implementation with the Tradesignal programming language Equilla.
To implement the algorithm in Tradesignal we first have to do the shown scatter plot. The algorithm stores the values in an array.
8/9 calculates the value of the fast and slow RSI indicators
12/13 looks what will happen on the day after (for the training data set)
16/17/18 stores everything in an array.

The next task to complete is to calculate the distances of today’s RSI point to all the historic points in the training data set.

23/27 calculates the euclidean distance of today’s point to all historic points, line 29 then creates a sorted list of all these distances to find the k nearest historic data points in the training data set.
Nearly done. The next step is just to find out what classification (colour) the nearest points have got and use this information to create a prediction for tomorrow. This is done in lines 33 to 35

Have a look at the scatter chart at the beginning. If this would be the data stored in our training data set, the prediction, using the 5 nearest neighbours, would be -5. All the 5 nearest neighbours of our current data point are red.
Now that we got a prediction for tomorrow, we need to make use of this prediction and trade it. The returns then will show if everything works as predicted.
Over here I just do a simple long/short interpretation of the prediction, but of course you could also use the quality of the prediction (+5 or +1?) in some sort of way. Position sizing…?

kNN algorithm performance
The next chart shows 2000 bars of daily Brent data. It uses a 14 and 28 day RSI to predict the next day’s move in the Brent oil market. The training was on the first half of the data set, and the 5 nearest neighbours did the classification.
Underneath the chart the returns of this test are shown. (strategy equity). On the bottom of the char you see the two RSI indicators used for the generation of the prediction / buy-sell command.

kNN algorithm – conclusion
The kNN algorithm offers a framework to test all kind of indicators easily to see if they have got any predictive value. Judging on the shown graph it seems to work. It seems to be possible to use these two RSI indicators to predict tomorrow’s Brent move.
But unfortunately this also could be just completely useless curve fitting. It is you who has to select the indicators and their periods and you will have to define if you like the outcome of a selected parameter set. To many degrees of freedom to be sure. The kNN algorithm is useful, but its application in finance has to be treated carefully. Otherwise bad surprises are guaranteed
Not everything can be done by brute force, inspiration and experience are key factors in finance…
The analysis has been done using the tradesignal software suite.
Using Autocorrelation for phase detection
Autocorrelation is the correlation of the market with a delayed copy of itself. Usually calculated for a one day time-shift, it is a valuable indicator of the trendiness of the market.
If today is up and tomorrow is also up this would constitute a positive autocorrelation. If tomorrows market move is always in the opposite of today’s direction, the autocorrelation would be negative.
Autocorrelation and trendiness of markets
If autocorrelation is high it just means that yesterdays market direction is basically today’s market direction. And if the market has got the same direction every day we can call it a trend. The opposite would be true in a sideway market. Without an existing trend today’s direction will most probably not be tomorrows direction, thus we can speak about a sideway market.
Autocorrelation in German Power
But best to have a look at a chart. It shows a backward adjusted daily time series of German Power.

The indicator shows the close to close autocorrelation coefficient, calculated over 250 days. You will notice that it is always fluctuating around the zero line, never reaching +1 or -1, but let`s see if we can design a profitable trading strategy even with this little bit of autocorrelation.
The direction of autocorrelation
Waiting for an autocorrelation of +1 would be useless. There will never be the perfect trend in real world data. My working hypothesis is, that a rising autocorrelation means that the market is getting trendy, thus a rising autocorrelation would be the perfect environment for a trend following strategy. But first we have to define the direction of the autocorrelation:

To define the direction of the autocorrelation I am using my digital stochastic indicator, calculated over half of the period I calculated the autocorrelation. Digital stochastic has the big advantage that it is a quite smooth indicator without a lot of lag, thus making it easy to define its direction. The definition of a trending environment would just be: Trending market if digital stochastic is above it`s yesterdays value.
Putting autocorrelation phase detection to a test
The most simple trend following strategy I can think about is a moving average crossover strategy. It never works in reality, simply as markets are not trending all the time. But combined with the autocorrelation phase detection, it might have an edge.

Wooha! That`s pretty cool for such a simple strategy. It is trading (long/short) if the market is trending, but does nothing if the market is in a sideway phase. Exactly what I like when using a trend following strategy.
To compare it with the original moving average crossover strategy, the one without the autocorrelation phase detection, you will see the advantage of the autocorrelation phase filter immediately: The equity line is way more volatile than the filtered one and you got lots of drawdowns when the market is sideways.

Stability of parameters
German power has been a quite trendy market over the last years, that`s why even the unfiltered version of this simple trend following strategy shows a positive result, but let`s have a test on the period of the moving average.
Therefore I calculated the return on account of both strategies, the unfiltered and the autocorrelation filtered, for moving average lengths from 3 to 75 days.

Return on account (ROA) =100 if your max drawdown is as big as your return.
The left chart shows the autocorrelation filtered ROA, the right side the straight ahead moving average crossover strategy. You don`t have to be a genius to see the advantage of the autocorrelation filter. Whatever length of moving average you select, you will get a positive result. This stability of parameters can not be seen with the unfiltered strategy.
Autocorrelation conclusion:
Trend following strategies are easy to trade, but only make sense when the market is trending. As shown with the tests above, autocorrelation seems to be a nice way to find out if the market is in the right phase to apply a trend following strategy.
Ranking: percent performance and volatility
When ranking a market analysts usually pick the percent performance since a given date as their key figure. If a stock has been at 100 last year and trades at 150 today, percent performance would show you a 50% gain (A). If another stock would only give a 30% gain (B), most people now would draw the conclusion that stock A would have been the better investment. But does this reflect reality?
Percent Performance and Volatility
In reality and as a trader I would never just buy and hold my position, I would always adjust my position size somehow related to the risk in it. I like instruments that rise smoothly, not the roller coaster ones which will only ruin my nerves. So ranking a market solely by percent performance is an useless statistic for me.
Lets continue with our example from above: if stock A, the one who made 50% has had a 10% volatility, and stock B, the 30% gainer, only had a 5% volatility, I surely would like to see stock B on top of my ranking list, and not the high vola but also high gain stock A.
Risking the same amount of money would have given me a bigger win with stock B.
Combining Performance and Volatility
To get stock B up in my ranking list I will have to combine the absolute gain with the market volatility in between. This can be done quite simple. Just add up the daily changes of the stock, normalized by market volatility.Have a look at the formula of this new indicator:
index(today)=index(yesterday)+(price(today)-price(yesterday))/(1.95*stdev(price(yesterday)-price(2 days ago),21))
In plain English: Today’s Vola Return Index equals yesterdays Vola Return Index plus the daily gain normalized by volatility
So if the index has been at 100, the volatility (as a 95% confidence interval over 21 days) is 1 and the stock made 2 points since yesterday, then today’s index would be 100 + 2/1 = 3
Vola Return Index vs. Percent Return Index
Lets have a look at a sample chart to compare the 2 ranking methods. I therefore picked the J.P.Morgan stock.

The upper indicator shows you a percent gain index. It sums up the daily percent gains of the stock movement, basically giving you an impression what you would have won when you would have kept your invested money constant.
The indicator on the bottom is the Vola Return Index. It represents your wins if you would have kept the risk invested into the stock constant. (=e.g. always invest 100$ on the 21 day 95%confidence interval of the daily returns)
Have a closer look at the differences of these two indicators up to October 2016. JPM is slightly up, and that`s why the percent change index is also in the positive area. During the same time the Vola Return Index just fluctuates around the zero line, as the volatility of JPM picked up during this period of time. To keep your risk invested constant over this period of time you would have downsized your position when JPMs volatility picked up, usually during a draw down. No good.

The same can be observed on the upper chart, showing the last months movements of the index. Right now, after the recent correction the percent change index is, like the JPM stock, up again. On the other side the Vola Return Index is still down, due to the rising volatility in JPM.
Vola Return Index – Ranking
Lets put this to a test and rank the 30 Dow Jones industrial stocks according to the percent return index and using my Vola Return Index as a comparison, calculated since 01/01/2015.
The first three stocks are the same, they got the highest vola and highest percent return. But JPM and Visa would get a different sorting. Just see how low the JPM Vola Index is, it would not be the 4th best stock.

Percent returns says JPM and Visa are abou the same, only the Vola Return Index shows that VISA would have been the better investment vehicle compared to JPM. But see for yourself on the chart…

Conclusion
Make sure your indicators show what you actually can do on the market. There is no use in just showing the percent gains of a stock if you trade some kind of VAR adjusted trading style.
Keeping you risk under control is one of the most important things in trading, and using the Vola Return Index instead of just plotting the percent performance can give you some key insights and keep you away from bad investment vehicles. Also have a look at this stock picking portfolio based on similar ideas.
Tradesignal Equilla Code for Vola Return Index:

Position sizing – the easy way to great performance
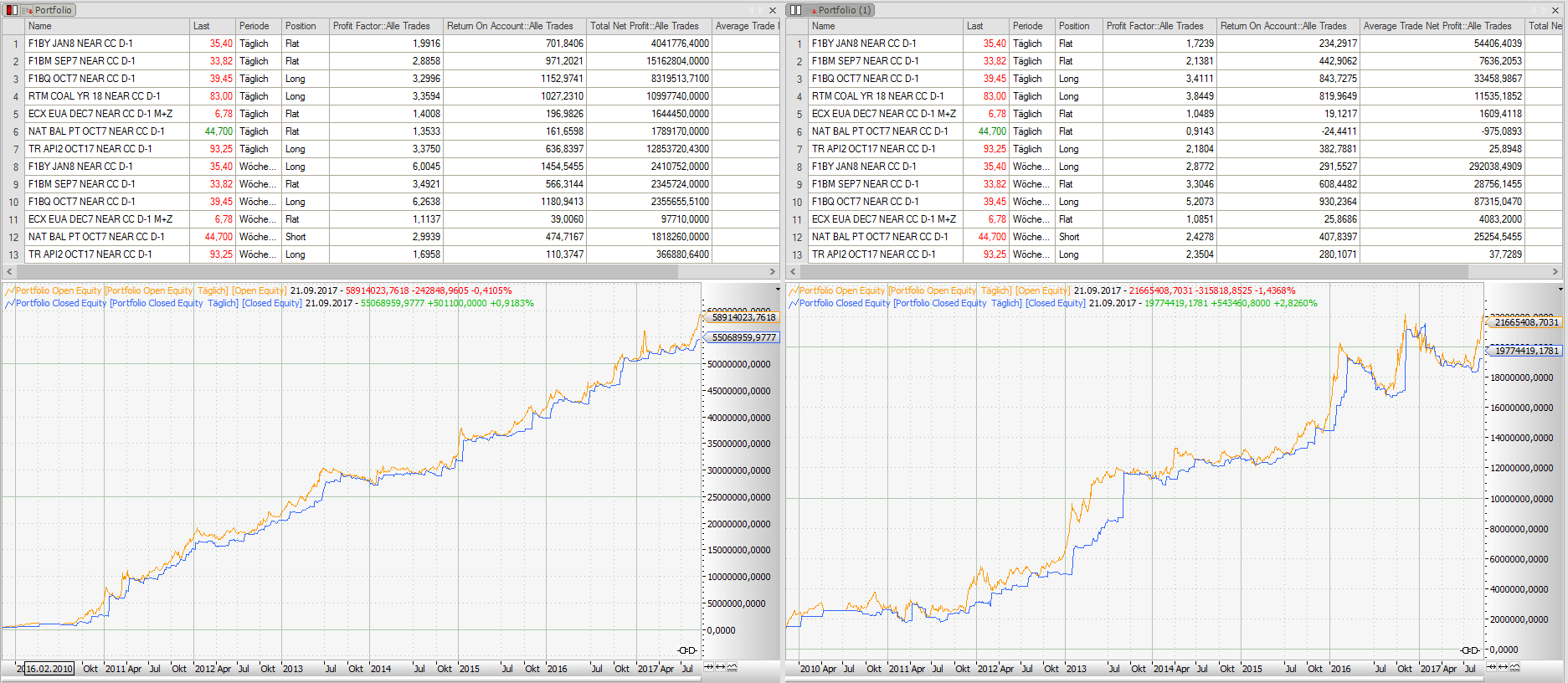
Working on your position sizing algorithm is an easy way to pimp an existing trading strategy. Today we have a look at an energy trading strategy and how the position sizing can influence the performance of the strategy.
The screenshot shows you the returns of the same trading strategy, trading the same markets, the same time frames and using the same parameters. The returns on the left side look nice, making money every year. The returns on the right side are somehow shaky, and you would have to love volatility of returns if you would think about trading this basket. The only difference between the basket on the right and on the left side is the position sizing.
The energy basket:
The basket trades German power, base and peak (yearly, quarterly, monthly), coal, gas, emissions. All instruments are traded on a daily and weekly time frame chart, using the same parameters. If the daily trading uses a 10-period parameter, the weekly trading would use a 10-week parameter. This limits the degrees of freedom I have when doing the strategy-time frame-parameter merge, thus minimizing the curve fitting trap.
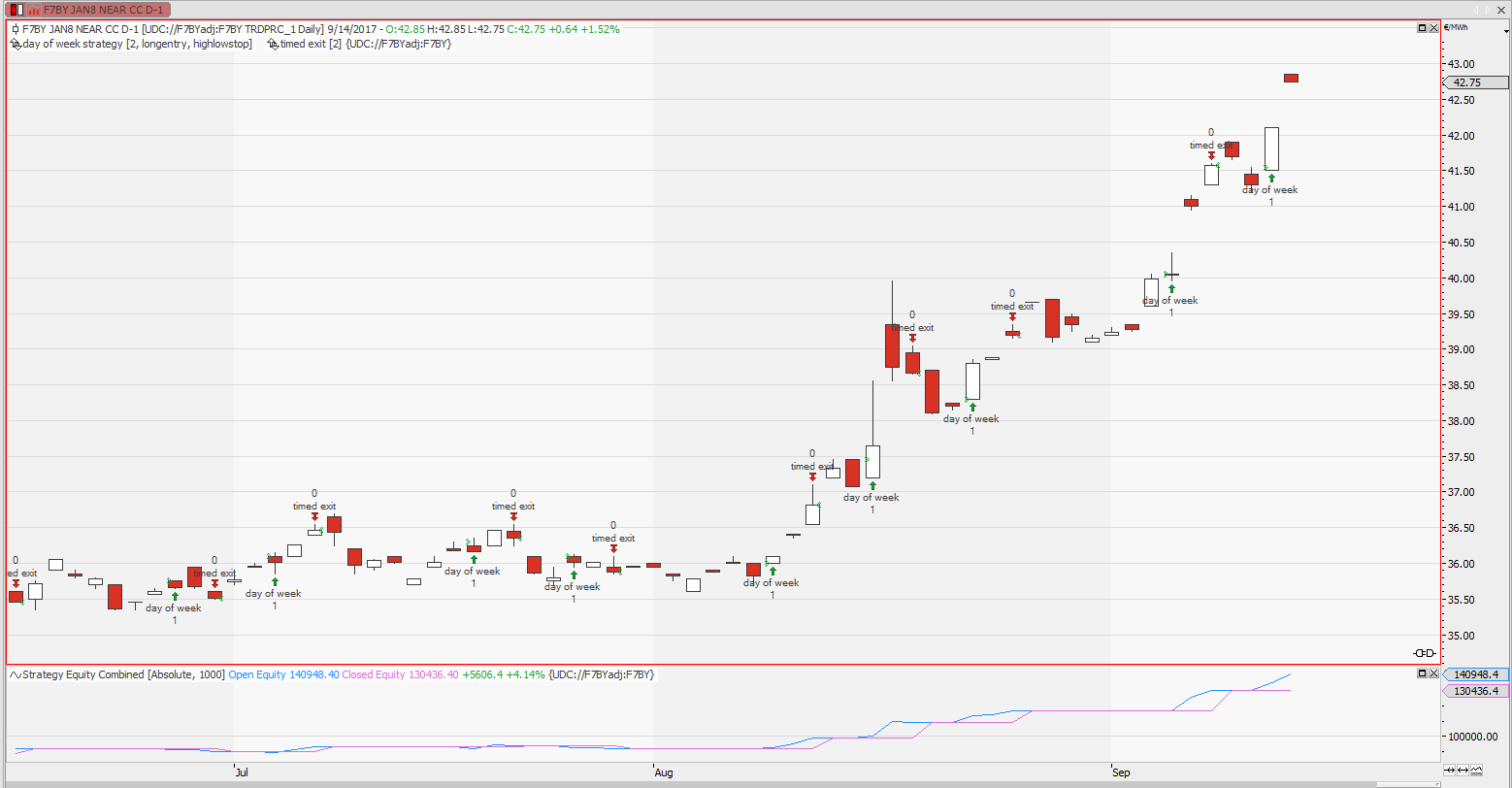
EEX Phelix Base Yearly – Buy Wednesday, short Thursday?
When it comes to simple trading strategies, the day of the week is surely one of the best things to start with. That’s nothing new when it comes to equity markets. Everybody knows about the calendar effects, based on when the big funds get and invest their money. I do not know about any fundamental reason for the day-of-week effect in German power trading, but is seems to be a fruitful approach.
First of all I have to point out that it is not only the day of the week which is important. A strategy that just buys on Wednesdays and sells 1 or 2 days later would be doomed. But if you add a little filter which confirms the original idea, you will end up with a profitable trading strategy.
This filter will just be a confirmation of the expected move: If you suspect that Wednesday ignites a bullish movement, then wait until Thursday and only buy if the market exceeds Wednesdays high. Same for the short side, wait for a new low before you enter!
Have a look at the chart. The strategy shown buys on Thursdays if Wednesdays high is exceeded. The position is closed 2 days after the entry.
If you run a simple test which day of the week is the best to get ready for a long trade the day after then the next chart shows the return on account of the strategy using data from 2012 up to now: (exit one day after entry)
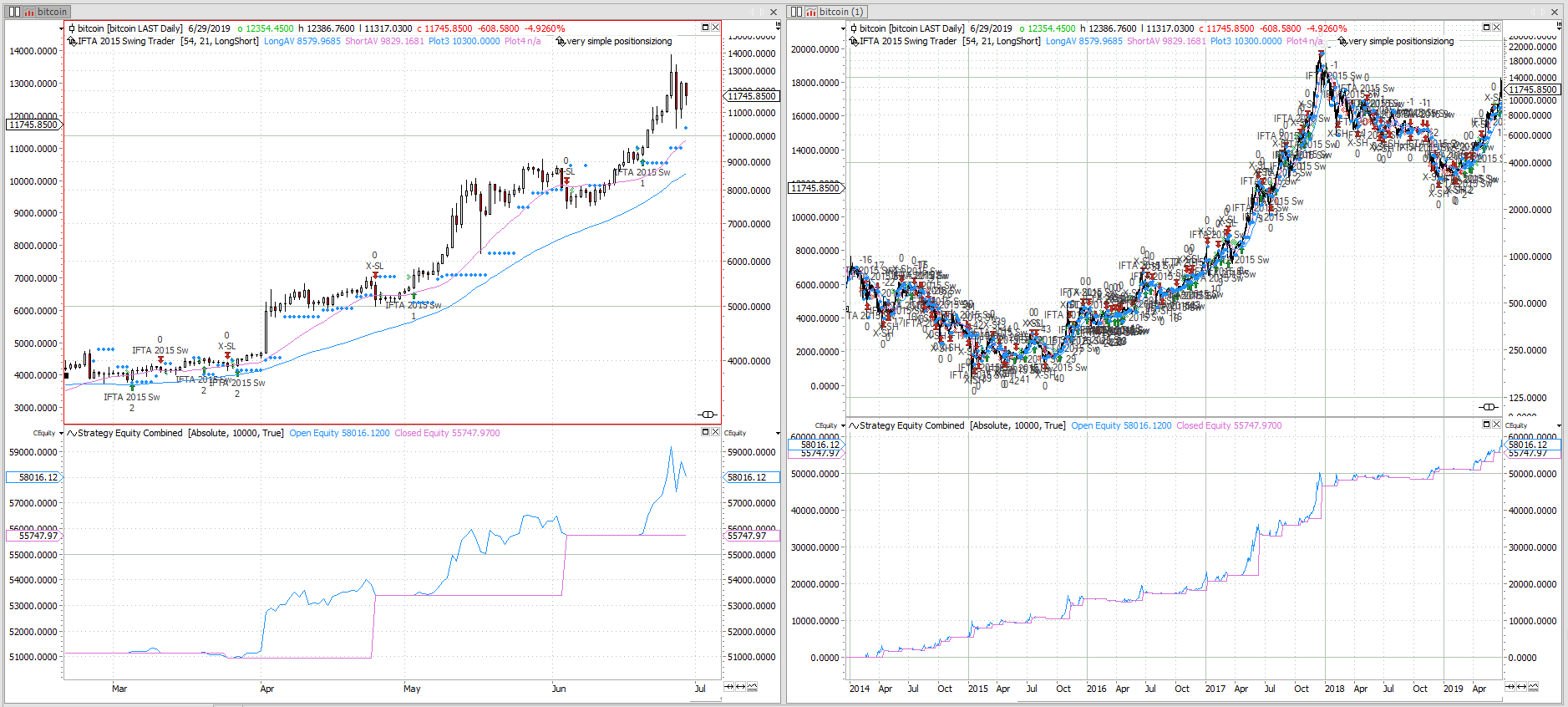
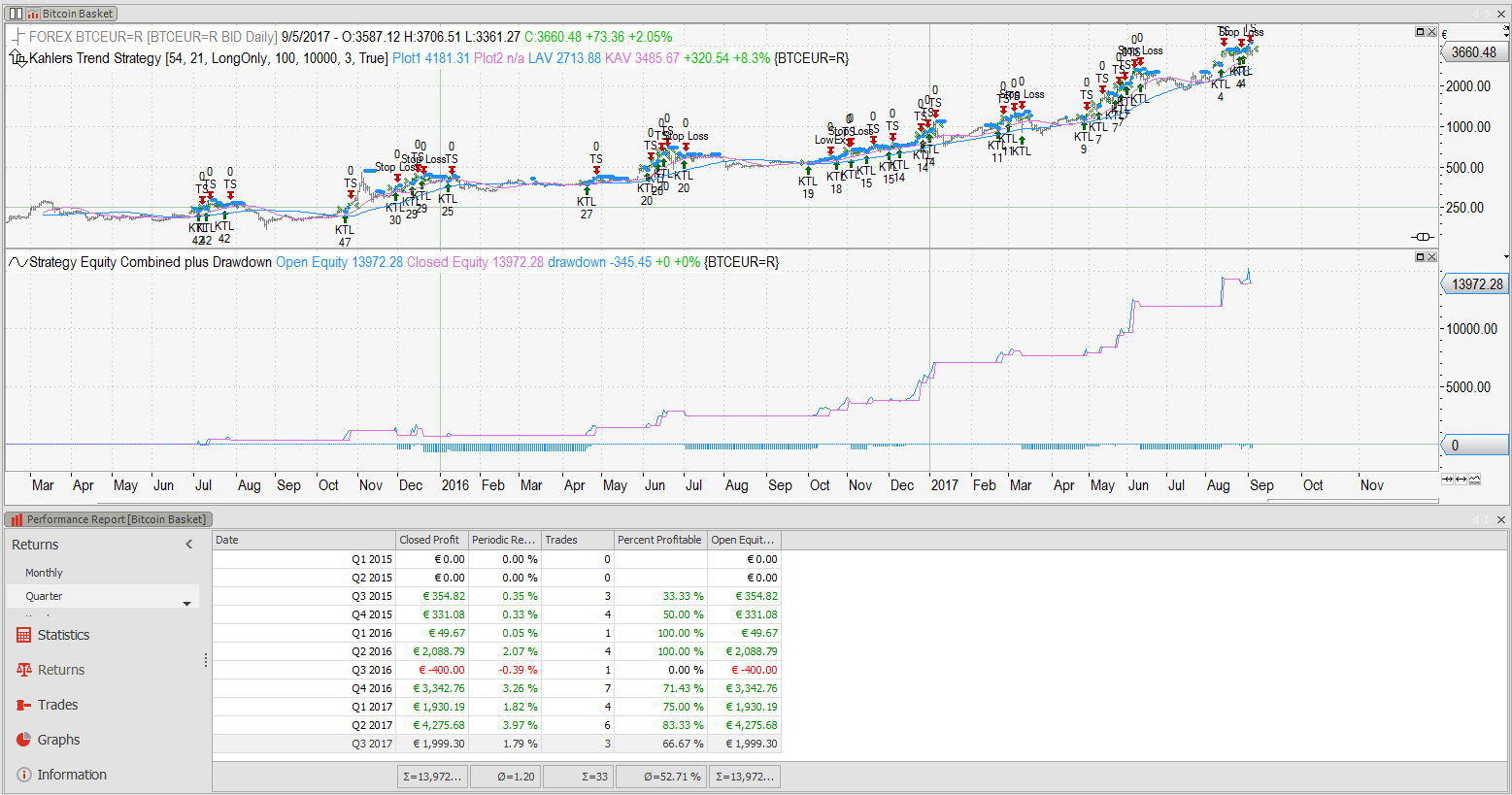
Bitcoin Trading Strategy – review of returns
Bitcoin is not as bullish as it used to be. May it be due to fundamental reasons like transaction cost and slow speed, or maybe the herd found a new playground, whatever it might be, it is a good time to have a look how my bitcoin trading strategy performed.
The bitcoin trading strategy uses two moving averages for the trend detection, and, when the averages say bullish, the strategy will buy if the market moves above it`s old swing high.
The position is protected with an exit at the last swing low and a 3% trailing stop.
But have a look how this simple strategy performed over the last two years:
Trading on a daily timeframe and investing 10000€ with each entry, the strategy managed to get more than a 100% return over the last 2 years.
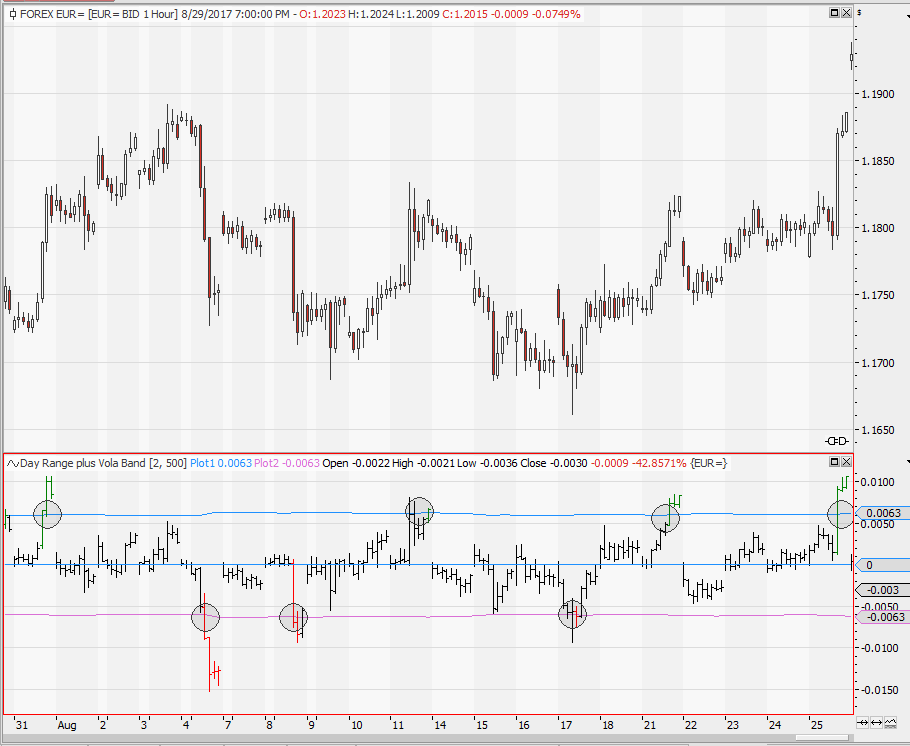
The rhythm of the market
Usually we chart the market at it’s absolute level. But what, if we would just chart the net daily, weekly, monthly movement? Would this be an advantage? Would this show us new trading opportunities?
The short answer is: Yes! The trend is not everything, and it seems to be of some significance for further movements, if the market has moved more than x % from the beginning of the day, week or month.
But let’s have a look at some charts – and you will see how well it works:
The first chat is an intraday chart of EuroDollar, 8am-5pm CET. It shows you the daily net movement.
Opening Range Breakout
Das Opening Range Breakout System wurde im Magazin “Technical Analysis of Stocks&Commodities” im Juli 1994 besprochen, und wie es scheint, funktioniert es, zumindest ohne slippage uns Speasen, noch immer.
Ein Opening Range Breakout System von Perry Kaufmann.
Es wurde im Magazin “Technical Analysis of Stocks&Commodities” im Juli 1994 besprochen, und wie es scheint, funktioniert es noch immer. (ohne slippage) Auch Tony Crabel schrieb zu diesem Opening Breakout System im selben Magazin
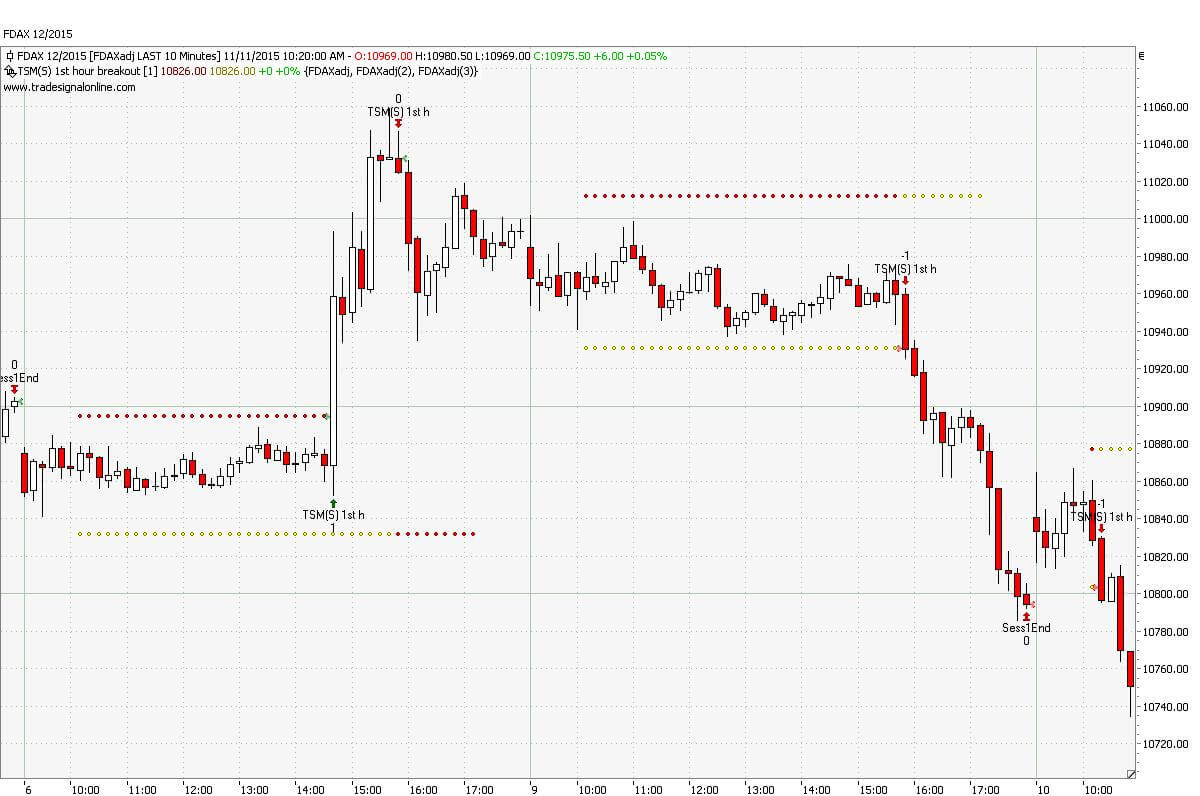
Das System wartet die erste Handelsstunde ab und geht dann bei Erreichen eines neuen Hochs oder Tiefs long oder short. Die Einstiegs Order (Stop Buy / Stop Sell) wird nicht exakt auf das Hoch / Tief gelegt, sondern ein paar Punkte darüber /darunter. (hier 20 Ticks)
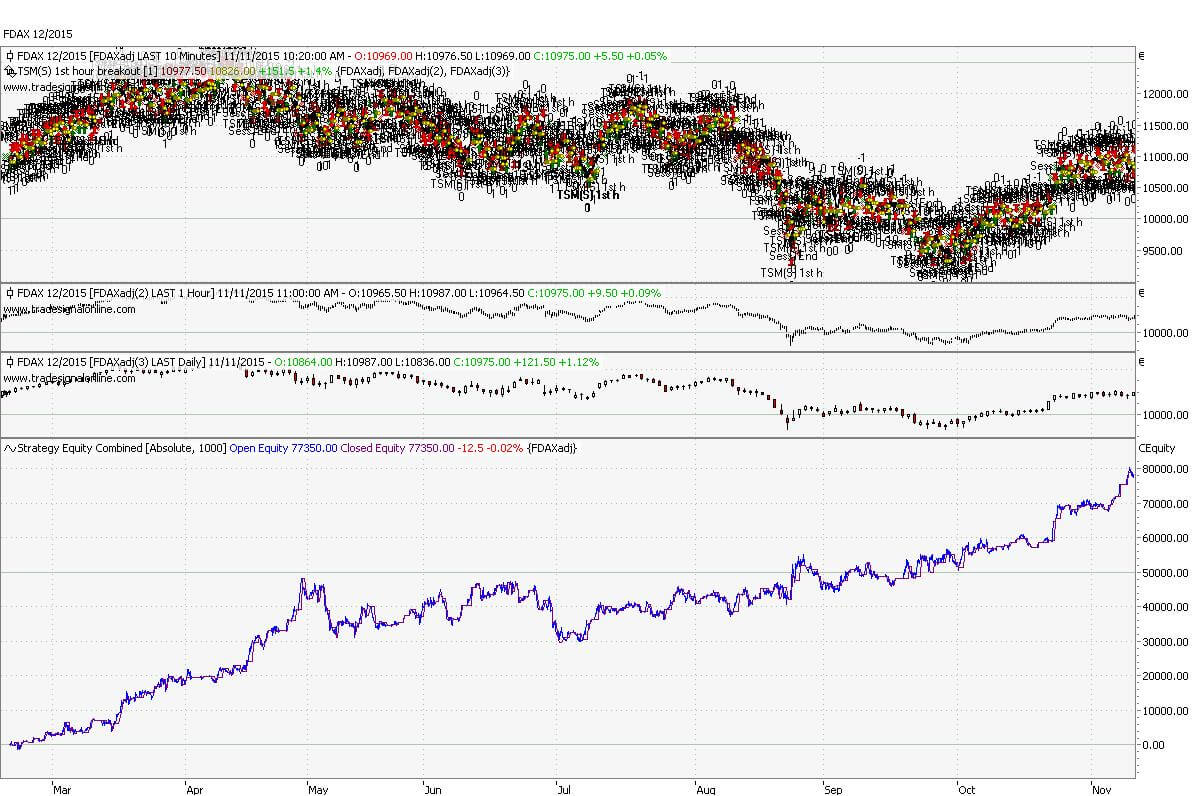
Tradesignal Programmierung des Opening Range Systems
Durch das laden von drei Zeitreihen, 10min, Stunden- und Tagesdaten gestaltet sich die Programmierung sehr einfach. Dies schränkt jedoch die Flexibilität deutlich ein.
Prinzipiell ist die Strategie der Afternoon Trader Strategie sehr ähnlich, sie weist auch mehr Flexibilität in der Programmierung auf. Auch der Artikel über Range Breaks im intraday Markt basiert auf einer ähnlichen Idee.
Da die hier vorgestellte Systemversion ursprünglich für dieTradestation 2000i in Easy Language geschrieben wurde, ist das Laden von 3 Zeitreihen ein wenig kompliziert gelöst. Aber es funktioniert.