When developing a new trading strategy you are usually confronted with multiple tasks: Design the entry, design the exit and design position sizing and overall risk control. This article is about how you can test the edge of your entry signal before thinking about your exit strategy. The results of these tests will guide you to the perfect exit for the tested entry signal (entry-exit combination) Continue reading
Indicator
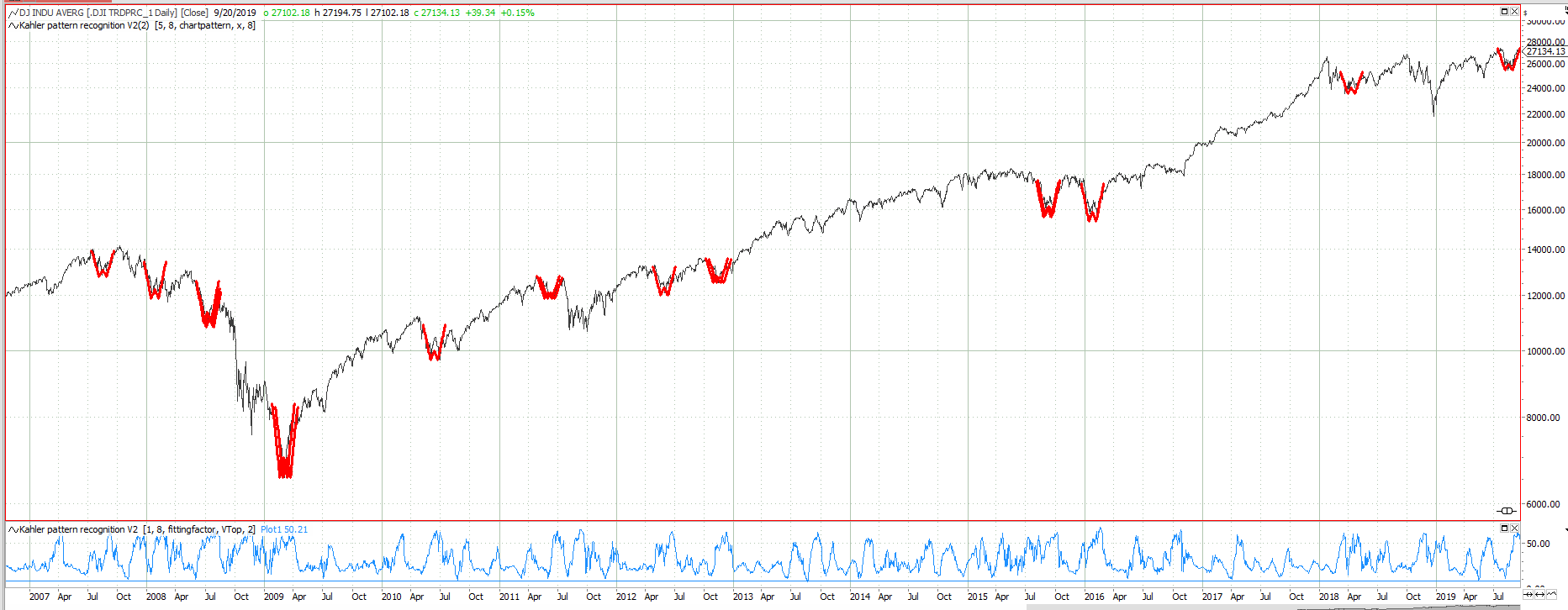
A simple algorithm to detect complex chart patterns
Finding complex chart patterns has never been an easy task. This article will give you a simple algorithm and a ready to use indicator for complex chart pattern recognition. You will have the freedom to detect any pattern with any pattern length. It has been described as Fréchet distance in literature. This article shows a simple adaption for chart pattern analysis.
Defining a chart pattern
The Edge of Technical Indicators
Classical technical indicators like RSI and Stochastic are commonly used to build algorithmic trading strategies. But do these indicators really give you an edge in your market? Are they able to define the times when you want to be invested? This article will show you a way to quantify and compare the edge of technical indicators. Knowing the edge of the indicator makes it an easy task to select the right indicator for your market. Continue reading
Noisy Data strategy testing
Algorithmic trading adds noise to the markets we have known. So why not add some noise to your historic market data? This way you can check if your algorithmic trading strategies are fit for the future. Learn how to generate noisy data and how to test your strategies for stability in a noisy market.
Synthetic market data?
Monte Carlo Simulation of strategy returns
Monte Carlo Simulation uses the historic returns of your trading strategy to generate scenarios for future strategy returns. It provides a visual approach to volatility and can overcome limitations of other statistical methods.
Monte Carlo Simulation
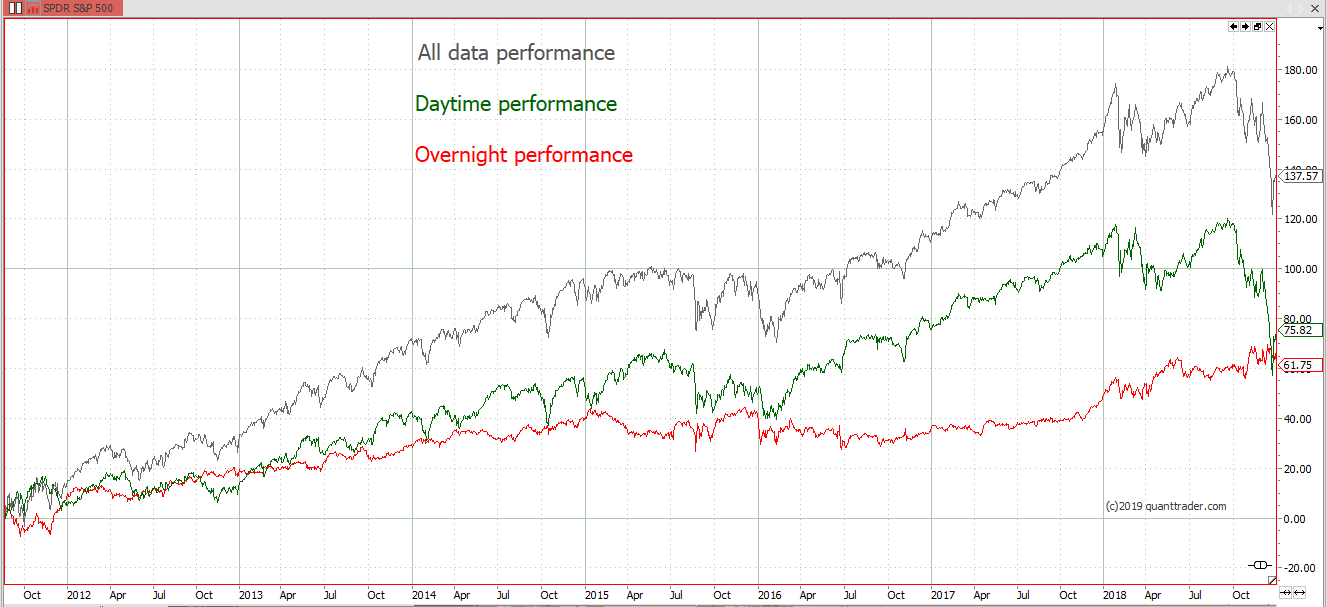
Overnight vs Daytime Performance & Volatility
Analysing the market performance of the day session vs. the overnight movement reveals some interesting facts.
Daytime vs. Overnight Performance
Bullish? Buy stock or sell put option?
So you are bullish on a specific stock, but you also have realised that timing is major problem? So what would be the best strategy to implement your bullish opinion but avoid the problems of any timing strategy?
Selling a put option might be the answer. Continue reading
Technical vs. Quantitative Analysis
“The stock market is never obvious. It is designed to fool most of the people, most of the time” Jesse Livermore Continue reading
Market crash or market correction?
Over the last days and weeks some traders have been worried if the currently ongoing correction in the markets will evolve into a crash, or if it is just a normal correction. Continue reading
Bollingerband: The search for volatility
Usually it makes no sense to fight against normal distribution. But there are setups which have got a high probability of unexpected behaviour. Volatility can be the key to future market movements. Continue reading
Weis Wave indicator code for Tradesignal
The Weis Wave indicator combines trend and volume information. It seems to be of some interest for timing short term market reversals. Here comes a version of this indicator for usage in Tradesignal. Continue reading
Tradesignal Implied Volatility and IV Percentile Scanner
Implied volatility data is key in options trading. This article shows how to access free volatility data in the Tradesignal software suite. Continue reading
IV Percentile – when to sell volatility
Volatility trading: when to buy and when to sell volatility Continue reading
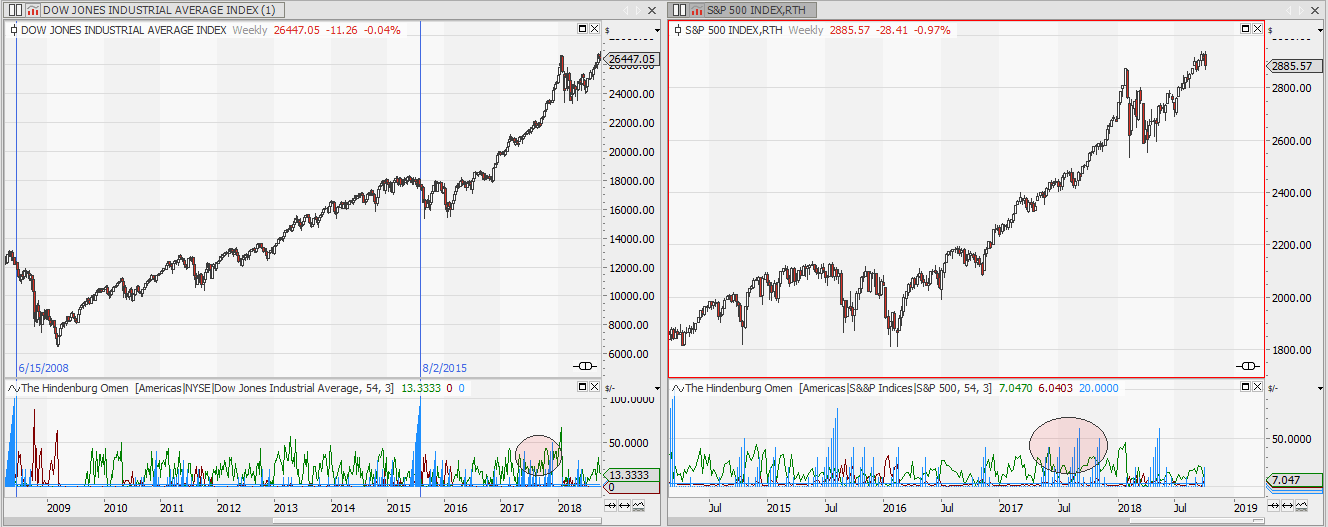
The Hindenburg Omen – Stock Market Crash Ahead?
The Hindenburg Omen is an indicator which is believed to forecast market crashes. Unfortunately it does not work, but the idea behind this indicator is worth to be discussed. Continue reading
Distribution of Returns
“Tomorrow never happens. It’s all the same fucking day, man. ” Janis Joplin Continue reading
Bet on Bollinger
Ever since John Bollinger introduced his Bollinger Bands in the early 1980s the bands have been a favourite indicator to all technical trades. This article is about the prediction capabilities of Bollinger bands. Continue reading
Scanning for Support and Resistance Probabilities
I have been in search for a signal I could use for a short vertical spread or naked short option strategy. So my main concern has been to find a level, which will most probably not be penetrated over the next few bars.
This is what I came up with. Continue reading
Backtesting Market Volatility
If you want to trade volatility, you can place a bet on the option market. Just buy an at the money put and call, and at expiry day you will either win or lose, depending on the actual market move since you bought the straddle and the price you paid for the straddle. To put it simple, if the market moves more than you paid for the two options you will win, otherwise you will lose. This article is about a back test of volatility. Continue reading
Demystifying the 200 day average
The 200 day average is considered as a key indicator in everyday technical analysis. It tells us if markets are bullish or bearish. But can this claim be proved statistically, or is it just an urban legend handed down from one generation of technical analysts to the next? Let’s find out and demystify the 200 day moving average. Continue reading
Seasonal trouble ahead
If a bitchy prime minister and a crazy president weren’t enough, for the upcoming months the seasonal chart is also indicating further price setbacks. Continue reading